A cura di Duilio Corradi
Premessa
Costruire modelli di navi è un hobby affascinante. Qualunque sia il tipo di nave scelto, il materiale usato e il risultato ottenuto, è sempre una pratica altamente gratificante.
Molti si impegnano nella costruzione di modelli naviganti e anch’io, molti anni fa, mi sono impegnato in questo senso.
Quel primo tentativo, nonostante la presunzione di capire qualcosa di navi, fallì miseramente: il modello aveva un equilibrio molto precario …e così divenne un modello “statico”, e statici furono altri modelli costruiti successivamente.
Poi, anni dopo, mi è tornata la voglia di ritentare il navigante e ho cominciato a costruire il Normandie.
Ma questa volta sono stato più attento e il modello non solo galleggia ma ha superato prove di stabilità anche molto severe.
Il mio hobby mi consente di entrare in contatto con altri modellisti, e amo condividere con loro il grande piacere che si prova quando il paziente lavoro è coronato da successo.
Ma se qualcosa non funziona soffro anch’io.
Purtroppo mi è capitato di vedere splendidi modelli che, posati in acqua, trovano difficoltà a galleggiare correttamente e a rimanere in equilibrio.
Ho così pensato di mettere a disposizione quella poca esperienza che ho fatto e rispolverare un po’ di quelle nozioni che, pur entrate a fatica nella mia zucca e in buona parte ormai fuggite, possono aiutare a comprendere e risolvere almeno i problemi principali.
Lascio perdere la complessa teoria che tratta della stabilità delle navi e provo a semplificare il tutto. Con molta probabilità scandalizzerò qualche esperto ma il mio scopo è soltanto quello di dare il mio piccolissimo contributo agli amici che vogliono far navigare i loro modelli.
IL DISLOCAMENTO
Tutti conoscono, certamente, la storiella del buon Archimede che, entrato nella vasca da bagno, si è sentito spingere verso l’alto. Ha cioè scoperto che “un corpo immerso nell’acqua riceve una spinta, dal basso verso l’alto, pari al peso del volume dell’acqua spostata”.
Per la verità le navi galleggiavano già prima della nascita di Archimede, ma questa è un’altra storia. Noi ci accontentiamo di sapere che quando prendiamo in mano un modello sentiamo che ha un certo peso. Poi lo poggiamo sull’acqua e lui comincia ad immergersi fino a raggiungere una condizione di equilibrio. A questo punto il modello “galleggia”. E’ questa la condizione in cui il peso del volume dell’acqua spostato dalla carena del modello è uguale al peso del modello stesso.
Possiamo così affermare che
il “dislocamento” corrisponde al “peso” della nave
Possiamo aggiungere che il peso del volume dell’acqua spostata dipende anche dal peso specifico dell’acqua medesima. Nell’acqua di mare, più densa, il modello si immergerà meno di quanto fa nell’acqua dolce.
Un modello riproduce, di solito, una nave esistente o esistita, con la sua brava “linea di galleggiamento”. Il modello dovrà naturalmente avere un peso adeguato, rispetto al volume della sua carena, in modo da raggiungere l’equilibrio dopo essersi immerso fino a quella linea.
Se non si immerge a sufficienza si possono aggiungere pesi. Se si immerge troppo …ahi, ahi.
EQUILIBRIO DEI CORPI GALLEGGIANTI
Un modello, esattamente come una nave vera, una volta nell’acqua in condizioni di galleggiamento, deve rimanere in equilibrio, cioè dritto. Se comincia a pendere da una parte, o se è troppo appoppato o appruato, e nonostante lo spostamento di qualche peso risulta molto difficile metterlo in equilibrio, abbiamo “sbagliato” la costruzione, ovvero non abbiamo rispettato alcune regole fondamentali che adesso cerco di descrivere nel modo più semplice che posso.
Trascuro, naturalmente, le conseguenze dovute alla forma stellata della carena, diversa fra poppavia e proravia, nonché le conseguenze della variazione di forma della parte immersa in seguito alle oscillazioni combinate, trasversali e longitudinali, dello scafo.
Stabilità trasversale
Un modello che, dopo aver subito uno spostamento in senso trasversale, torna a raddrizzarsi, ha un equilibrio stabile
Se invece non ci riesce, ha un equilibrio indifferente
Se tende a capovolgersi, ha un equilibrio instabile
Ciò premesso vediamo di capire come si comportano le forze in gioco (ripeto, semplificando al massimo i concetti).
Abbiamo visto che il nostro modello ha un peso che chiamiamo D e lo rappresentiamo con una freccia rivolta verso il basso applicata nel punto G che è il centro di gravità del nostro modello.
Quando il modello è in acqua, in condizione di galleggiamento, subisce una serie di spinte verso l’alto, su tutta la carena, che noi rappresentiamo come un’unica spinta applicata nel punto C (centro di carena). Questa spinta, che chiamiamo S, è rivolta verso l’alto ed è naturalmente uguale ed opposta a quella che indica il peso (D).
Un precisazione, prima che qualcuno protesti. Effettivamente la spinta S, nel disegno, non è applicata in C bensì in C 1. Tenete presente che, a modello dritto sia la freccia D che la freccia S sono perpendicolari alla linea di galleggiamento A-B, uguali e contrapposte lungo l’asse di simmetria della nave. Perdonatemi ma è solo per non pasticciare troppo il disegno. Fra poco sarà tutto più chiaro.

Adesso diamo una ditata al nostro modello e costringiamolo ad abbattersi un po’ su un fianco.
Cioè lo costringiamo a passare dal galleggiamento A-B al galleggiamento A1-B1 (sempre per semplicità grafica è stato meglio spostare l’acqua e non il modello).
Cosa abbiamo combinato?
Il centro di gravità G è sempre nello stesso posto e la freccia D, che rappresenta il peso, è ora perpendicolare alla nuova linea di galleggiamento A1-B1.
Il centro di carena C, invece, si è spostato nella posizione C1b>. Ed ecco che adesso la spinta S è applicata in questo nuovo centro di carena C1, naturalmente anche lei perpendicolare alla nuova linea di galleggiamento A1-B1.
Penso che tutto questo sia chiaro. Adesso possiamo passare ad individuare una serie di elementi che ci aiuteranno a capire come aiutare il nostro modello a starsene ben dritto in acqua.
>Innanzi tutto notiamo che le due forze D e S creano una coppia che tende a raddrizzare lo scafo.
Poi, attraverso il nuovo centro di carena C1, facciamo passare una linea tratteggiata, perpendicolare alla linea di galleggiamento, e prolunghiamola fino a farle incontrare l’asse di mezzeria della nave.
Il punto di incontro lo indichiamo con m. Questo punto è estremamente importante e si chiama metacentro.
Adesso guardiamo bene il disegno.
Prendiamo come riferimento la posizione del centro di carena C e l’altezza del centro di gravità G e del metacentro m rispetto a questo.
L’altezza di G su C la chiamiamo a.
L’altezza di M su C la chiamiamo r.
La differenza fra l’altezza r di m e l’altezza a di G è, naturalmente, r-a.
Questa differenza r-a si chiama altezza metacentrica.
Ora cerchiamo di fare un ragionamento pratico su cosa succede al modello.
La carena è quella che è e deve immergersi nell’acqua fino alla linea di galleggiamento.
Anche il peso complessivo del nostro modello è quello che è.
Dov’è il trucco?.
Semplice. Tutto sta nell’altezza del centro di gravità, o baricentro, del modello.
Più i pesi che lo compongono sono posti in basso più il centro di gravità G scende, più sono posti in alto più il centro di gravità sale.
Ma sali sali, se per caso arriva all’altezza del metacentro m, si annulla l’effetto raddrizzante delle forze D e S. Cioè il modello potrebbe ruotare su se stesso. Se addirittura salisse oltre, state pur sicuri che il modello si capovolge.
E’ tutto chiaro?
Allora ricordiamo che la regola fondamentale per assicurare al modello una buona stabilità consiste nel costruire il tutto il più leggero possibile (usando materiali leggeri e spessori al minimo indispensabile) e raggiungere il peso necessario (dislocamento) aggiungendo zavorra il più in basso possibile.
Assetto longitudinale
Abbiamo visto come sta dritto un modello. Ma il nostro capolavoro dovrà avere anche un corretto assetto longitudinale. Le immersioni a poppa e a prua dovranno essere quelle previste.
Una piccola nota pratica: le navi, di norma, navigano “leggermente” appoppate.
Anche qui è tutto un problema di distribuzione dei pesi nel senso della lunghezza della nave. Dovremo tenere conto di dove sono i pesi fissi. Ad esempio se costruiamo un modello con le sovrastrutture molto verso prua (o verso poppa), siamo certi che, in quella posizione, c’è tutto il loro peso. Cerchiamo, allora, di fare quattro conti posizionando al meglio, nel limite del possibile, motori e batterie, che costituiscono i pesi maggiori.
Ma la regola di realizzare una costruzione leggera vale anche in questo caso. La zavorra che possiamo poi imbarcare per abbassare il centro di gravità, la possiamo mettere più verso prua o più verso poppa in modo da ottenere l’assetto voluto.
Ho detto di “fare quattro conti”. Ma anche qui la cosa è tutt’altro che semplice. Per fortuna un modello non imbarca combustibili, lubrificanti, acqua potabile e acqua di lavanda. Non ha doppifondi e serbatoi sparsi dappertutto. Non ha consumi e non effettua spostamenti durante il viaggio. Ci possiamo quindi risparmiare tutto quel bordello di calcoli che quando andavo a scuola io, e i conti erano fatti a mano, facevano diventare matti (io, comunque, li sbagliavo sempre).
Però erano importanti. Pensate solo al caso di una nave che si incaglia. Bisogna disporre delle immersioni teoriche, di poppa e di prua, determinate in base ai consumi effettuati ed alla loro posizione, e confrontarli con i pescaggi rilevati dopo l’incaglio. Bisogna quindi spostare o sbarcare pesi, nel posto e nella quantità giusta, in modo da ridurre o eliminare quella che si chiama “reazione del fondo”, e quindi cercare di disincagliare la nave.
Torniamo con i piedi per terra, o meglio vicino alle nostre acque più tranquille.
Possiamo accontentarci di sapere cosa succede quando si mettono o si tolgono pesi più verso prua o più verso poppa.
Mi aiuterò, anche in questo caso, con un semplice disegno. Anche qui chiedo perdono agli esperti.
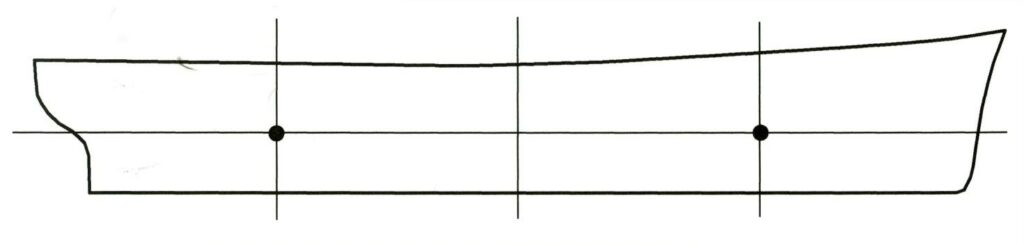
Immaginate di dividere il vostro modello in quattro parti (questa è una regola molto empirica, basti solo pensare alle diverse forme di carena, ma accontentiamoci).
Si individuano due punti, uno verso prora e uno verso poppa, che si chiamano “punti di indifferenza” o “punti neutri”.
Il modello è in condizione di galleggiamento.
Tenete a mente queste semplici regole:
Se si imbarca o si sbarca un peso in corrispondenza del punto neutro di poppa, l’immersione di poppa aumenta o diminuisce, mentre quella di prora resta invariata.
e si imbarca o si sbarca un peso in corrispondenza del punto neutro di prora, l’immersione di prora aumenta o diminuisce, mentre quella di poppa resta invariata.
Se si imbarca o si sbarca un peso fra i due punti neutri entrambe le immersioni aumentano o diminuiscono, in maniera diversa a seconda della posizione più verso prua o più verso poppa dell’operazione.
Se si imbarca o si sbarca un peso a poppavia del punto neutro di poppa, l’immersione di poppa aumenta o diminuisce mentre quella di prora diminuisce o aumenta.
Se si imbarca o si sbarca un peso a proravia del punto neutro di prua, l’immersione di prua aumenta o diminuisce mentre quella di poppa diminuisce o aumenta.
A vederle scritte sembrano difficili, ma non sono da imparare a memoria come una poesia. Un attimo di riflessione e tutto risulta chiaro …e indimenticabile.
Certo che, in questo modo, le variazioni di assetto si ottengono per tentativi e non per calcolo, ma per un modello può essere sufficiente.
Grazie a tutti per la pazienza …e per avermi fatto ricordare un po’ di antiche (per me) cose.
Ciao






